自学习蒙特卡洛方法 -- 通过提取描述系统低能有效模型的自学习过程，设计出优化的更新方法，克服量子多体系统蒙特卡洛模拟中临界慢化和接收概率低等瓶颈- - 自2016年提出以来，已经在凝聚态量子多体问题相变和临界现象研究中取得不少重要成果，受到广泛关注[1]。该方法在量子多体问题大规模数值计算领域中的应用，正在逐步深入[2, 3]。
　　伴随着石墨烯，尤其是最近魔角石墨烯体系中新的实验结果不断涌现，人们对于蜂窝晶格的相互作用狄拉克费米系统的性质越来越关心，如何准确刻画半金属、金属、绝缘体、超导体之间的量子相变以及量子临界区中非费米液体行为，正在变为更加重要的问题。
　　日前，中国科学院物理研究所/北京凝聚态物理国家研究中心博士生陈闯、研究员孟子杨与香港科技大学许霄琰博士，德国维尔兹堡大学 Martin Hohenadler 博士组成的研究团队，运用自学习蒙特卡洛和连续时间蒙特卡洛方法，研究了石墨烯蜂窝晶格上电声子耦合 Holstein 模型的相图，精确刻画了相互作用下的狄拉克费米子从半金属到电声耦合导致的绝缘体的相变过程，为理解狄拉克半金属的相变提供了新的思路和实例。该团队的研究成果，与来自加州大学戴维斯分校的另一支团队的独立工作，联袂发表在最近一期的 Physical Review Letters [4, 5]。

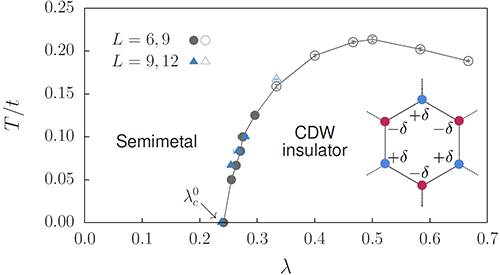图1. 狄拉克费米子 Holstein 模型相图，横轴为电声子耦合强度，纵轴为温度。耦合弱的时候，系统为狄拉克半金属（Semimetal）；耦合强时，声子的量子涨落引起电子有效吸引作用，狄拉克费米子局域化成为电荷密度波绝缘体（CDW insulator ）。由于 CDW 破缺 A,B 子晶格的 Z2 对称性，有限温度下的相变为 2D Ising 相变，零温的相变为 (2+1)D Gross-Neveu Ising 相变。

　　该团队选取半满的蜂窝晶格上狄拉克费米子与 Holstein 声子耦合的模型，声子部分具有本征振动频率和在虚时域的涨落，并与电子在格点上的电荷密度耦合，在电子之间引起有效相互作用，并在相变点附近将整个系统变成无法用微扰解析求解的强关联问题，只能通过数值求解。而Holstein 模型的量子蒙特卡洛模拟，由于声子本身的连续变量形式和其在虚时上的强烈相互作用，所导致的极长的自关联时间一直是领域中公认的难题，二维晶格系统的大规模计算模拟进展十分缓慢。自学习蒙特卡洛方法，找到了正确的声子有效模型，在有效模型的指引下蒙特卡洛更新的自关联时间大大缩短，在二维晶格的模型定量计算方面，已经取得重要的成果[3]。

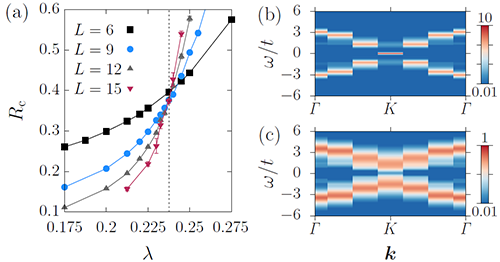图2. (a) 运用关联比（correlation ratio）确定半金属-CDW绝缘体量子相变的位置。系统尺度（L）越大，蒙特卡洛计算的难度也就越大。(b) 在半金属中的单粒子谱函数，在动量 K 点处没有能隙，线性色散的狄拉克费米子是稳定的。(c) 在 CDW 绝缘体中的单粒子谱函数，在动量 K 点处由声子的涨落引起电子之间的有效相互作用，打开了能隙。狄拉克费米子不复存在。

　　在本项目中，该团队用大规模量子蒙特卡洛计算给出了图1所示的相图。图中横轴为狄拉克费米子和声子的耦合强度，纵轴为温度。当耦合弱的时，狄拉克半金属稳定存在；当耦合强时，声子的量子涨落引起电子有效吸引相互作用，狄拉克费米子在相互作用之下变成电荷密度波绝缘体。由于 CDW 破缺 A,B 子晶格的 Z2 对称性，有限温度下的相变为 2D Ising 相变，零温的相变为 (2+1)D Gross-Neveu Ising 相变。为了精确研究有限温度的经典相变和零温的量子相变，该团队运用关联比（correlation ratio）和标度有限尺度数据坍缩（scaling collapse）等方式，确定临界点的位置和临界指数（如图2(a)），并通过蒙特卡洛和解析延拓结合的手段，计算了半金属和绝缘体中的单粒子谱，刻画了从无能隙的狄拉克半金属到有能隙的绝缘体的完整谱学行为变化（如图2(b), (c)）。
　　这项工作对于运用大规模蒙特卡洛方法研究石墨烯与类似晶格中的相互作用狄拉克费米子的性质打开了新的思路。掺杂之后的超导现象，以及超导和绝缘体之间的相变，还有量子临界区域中的反常输运行为等当前十分活跃的研究课题都可以在这个框架内进行探索。
　　这项工作得到了科技部重点研发计划2016YFA0300502，中科院先导项目 XDB28000000，国家自然科学基金委项目 11574359以及松山湖材料实验室的支持。量子蒙特卡洛模拟所需的大规模的并行计算在中科院物理所量子模拟科学中心和天津国家超算中心天河1号平台上完成，计算过程中得到了天津国家超算中心孟祥飞博士、菅晓东工程师等同事的有力配合，在此一并感谢。

参考文献
[1] 从德尔斐箴言到自学习蒙特卡洛，孟子杨，物理，46，248-252 （2017）

[2] Symmetry Enforced Self-Learning Monte Carlo Method Applied to the Holstein Model,
Chuang Chen, Xiao Yan Xu, Junwei Liu, George Batrouni, Richard Scalettar, Zi Yang Meng,
Phys. Rev. B 98, 041102(R) (2018)

[3] EMUS-QMC: Elective Momentum Ultra-Size Quantum Monte Carlo Method,
Zi Hong Liu, Xiao Yan Xu, Yang Qi, Kai Sun, Zi Yang Meng,
Phys. Rev. B 99, 085114 (2019)

[4] Charge-Density-Wave Transitions of Dirac Fermions Coupled to Phonons,
Chuang Chen, Xiao Yan Xu, Zi Yang Meng, Martin Hohenadler,
Phys. Rev. Lett. 122. 077601 (2019)

[5] Charge Order in the Holstein Model on a Honeycomb Lattice
Y.-X. Zhang, W.-T. Chiu, N.C. Costa, G.G. Batrouni, R.T. Scalettar,
Phys. Rev. Lett. 122. 077602 (2019)